勾股定理练习题,数学世界中的趣味探险
亲爱的数学爱好者们,你是否曾在某个午后,手握笔杆,沉浸在勾股定理的奇妙世界中?勾股定理,这个古老的数学定理,如同一位神秘的向导,引领我们探索直角三角形的奥秘。今天,就让我们一起踏上这场数学探险之旅,通过一系列有趣的勾股定理练习题,感受数学的魅力吧!
一、勾股定理的起源与魅力
勾股定理,又称为毕达哥拉斯定理,源于古希腊。相传,古希腊数学家毕达哥拉斯发现,直角三角形的两条直角边的平方和等于斜边的平方。这个看似简单的定理,却蕴含着无尽的奥秘。它不仅揭示了直角三角形边长之间的关系,还为我们打开了通往数学世界的另一扇大门。
二、勾股定理的练习题大挑战
1. 填空题:

- 在直角三角形ABC中,若AB=5,BC=12,且第三边c为奇数,且a、b、c都是3的倍数,则c应为______,此三角形为______。
- 三角形中两条较短的边为a、b,若a^2 - b^2 = ab,则当第三条边为______时,此三角形为直角三角形。
- 若直角三角形的三边a、b、c满足a^2b^2c^2 = 2506a 8b 10c,则此三角形是______三角形,面积为______。
2. 选择题:

- 给出下列几组数:8,15,16;n^2 - 1,2n,n^2 - 1;m^2 - n^2,2mn,m^2n^2(m≠0)。其中定能组成直角三角形三边长的是( )。
A. 8,15,16
B. n^2 - 1,2n,n^2 - 1
C. m^2 - n^2,2mn,m^2n^2
D. 以上都不对
- 下列各组数能构成直角三角形三边长的是( )。
A. 1,2,3
B. 4,5,6
C. 12,13,14
D. 9,40,41
3. 解答题:
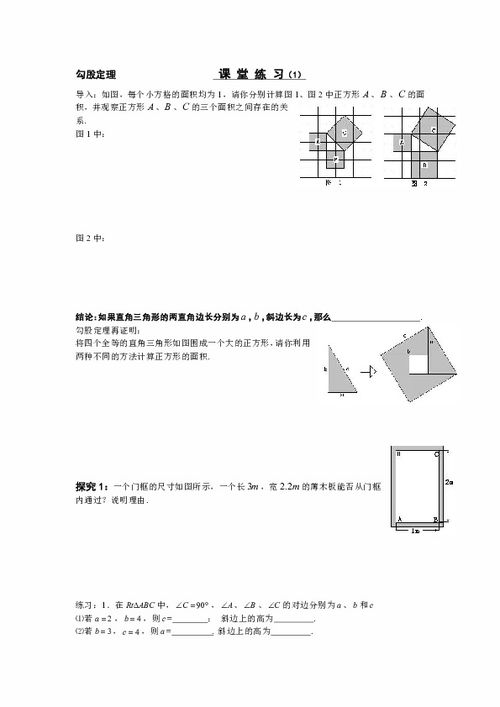
- 在直角三角形ABC中,D为BC上的一点,若AC=17,AD=8,CD=15,AB=10,求三角形ABC的周长和面积。
- 已知在直角三角形ABC中,BC=6,BC边上的高为7,若AC=5,则AC边上的高为______。
三、勾股定理的应用与拓展
勾股定理不仅在数学领域有着广泛的应用,还渗透到了生活的方方面面。以下是一些勾股定理的实际应用:
1. 建筑设计:在建筑设计中,勾股定理可以帮助工程师计算建筑物的结构稳定性。
2. 医学:在医学领域,勾股定理可以用于计算人体骨骼的长度和角度。
3. 地理测量:在地理测量中,勾股定理可以用于计算地球表面的距离和面积。
4. 军事:在军事领域,勾股定理可以用于计算火炮的射程和角度。
四、勾股定理的趣味拓展
1. 勾股数:满足勾股定理的三个正整数,称为勾股数。常见的勾股数有:3,4,5;5,12,13;6,8,10等。
2. 勾股定理的逆定理:若三角形的三边长分别是a,b,c,且满足a^2 b^2 = c^2,则三角形是直角三角形。
3. 勾股定理的变式:勾股定理的变式有很多,如a^2 - c^2 = b^2,b^2 - c^2 = a^2等。
五、
勾股定理,这个古老的数学定理,如同一位神秘的向导,引领我们探索直角三角形的奥秘。通过一系列有趣的勾股定理练习题,我们不仅感受到了数学的魅力,还学会了如何运用勾股定理解决实际问题。让我们一起继续探索数学的奇妙世界,发现更多有趣的数学定理吧!